9. Divisão por x – α

Em divisões na forma de A(x) por x – α, o resto é considerado como um número independente de x, que será simbolizado por r. 

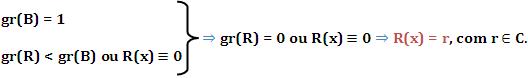
Em divisões x – α podemos obter o resto através do Teorema de D’Alembert, e o quociente e o resto através do Dispositivo Prático de Briot-Ruffini.

Teorema de D’Alembert

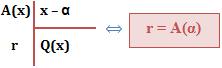
O valor numérico de A para x = α será considerado o resto da divisão do polinômio A por x – α.

Veja a representação:

Demonstração:

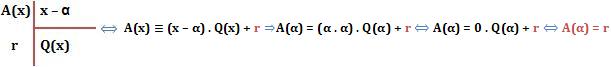
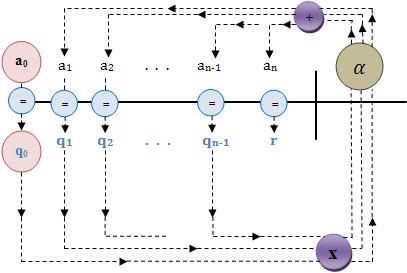
Obtenção do quociente e do resto

Através do Método de Descartes na divisão A(x) a0 . xn + a1 . xn-1 + a2 . xn-2 + … + an-1 . x + an, sendo a0 ≠ 0, por x – α, obtemos um quociente na forma de: 

Q(x) = q0 . xn-1 + q1 . xn-2 + q2 . xn-3 + … + qn-2 . x + qn-1, com q0 ≠ 0, e um resto na forma de R(x) = r.

Portanto:

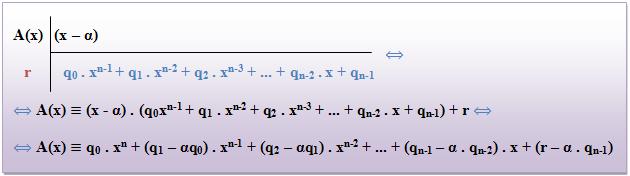
Ao igualar, de dois em dois, os coeficientes deste polinômio com os respectivos coeficientes iniciais de A(x), a0, a1, a2, …, an, temos:

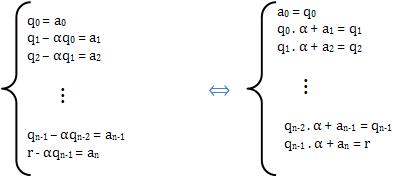
O significado do sistema anterior é a0 = q0 ou: 

(cada coeficiente de Q) . α + (próximo coeficiente de A) = próximo coeficiente de Q

O Dispositivo Prático de Briot-Ruffini está fundamentado nesta equação. Veja abaixo as fases

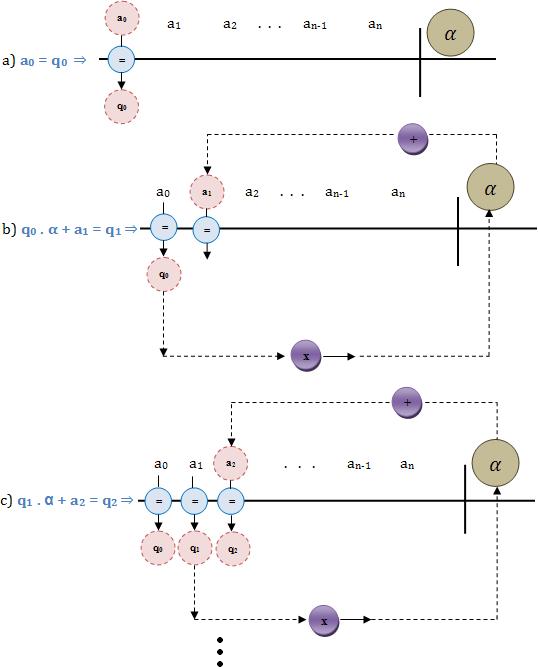
E assim sucessivamente. Sendo assim, partindo de a0 = q0, na direção da flecha obtemos q1, q2, q3, …, qn-1 e r.

Logo, o Dispositivo Prático de Briot-Ruffini é: