Relações em um triângulo qualquer
Por Redação
Relações em um triângulo qualquer
A trigonometria permite a determinação de elementos que não são dados de um triângulo, ângulos ou lados. Todos os cálculos dessas resoluções são fundamentados nas relações existentes nos elementos do triângulo. Vejamos agora a Lei dos senos e a Lei dos cossenos, que são consideradas as relações mais importantes.
• Lei dos Senos
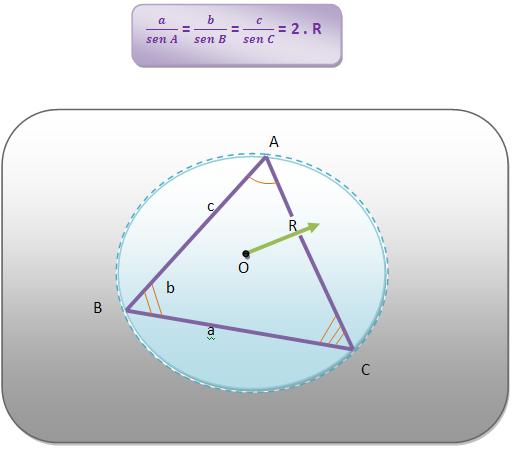
“Em todo triângulo, as medidas dos lados são proporcionais aos senos dos ângulos opostos e a razão de proporcionalidade é a medida do diâmetro da circunferência circunscrita ao triângulo”.
Considere o triângulo ABC, inscrito na circunferência de raio R:
Demonstração
Considere o triângulo ABC, inscrito na circunferência de raio R.

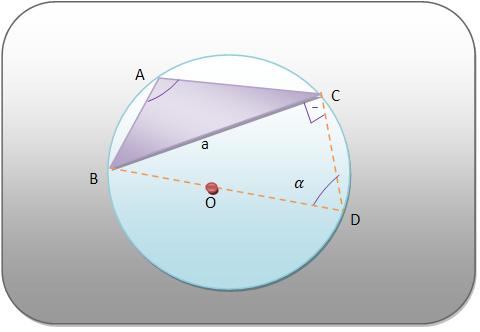

• Lei dos Cossenos
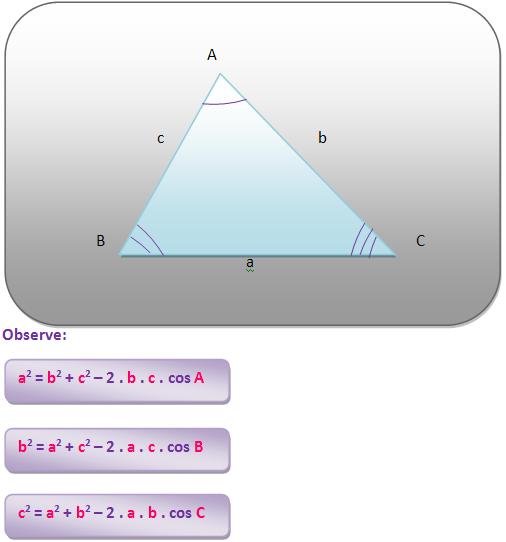
“Em todo triângulo, o quadrado da medida de um lado é igual à soma dos quadrados das medidas dos outros lados, menos o dobro do produto dessas medidas pelo cosseno do ângulo que eles formam”.
Considere o triângulo ABC, da figura.
Demonstração:
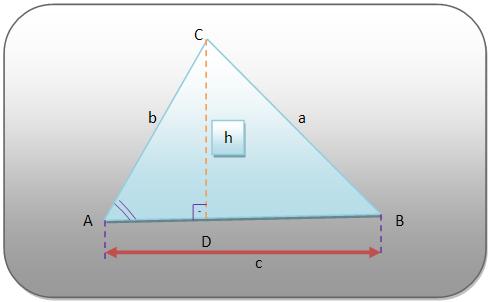
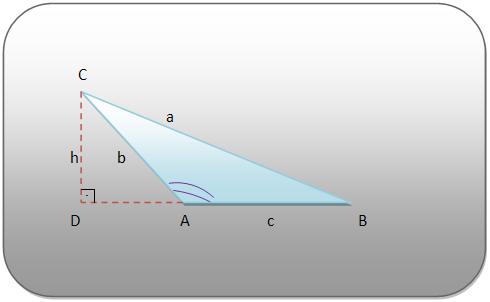
Veja que nos triângulo ABC das figuras, a altura relativa ao lado AB é h.

![]()
