Perpendicularismo
Por Redação
Perpendicularismo
Reta perpendicular ao plano
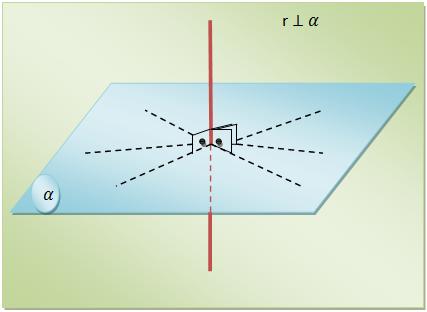
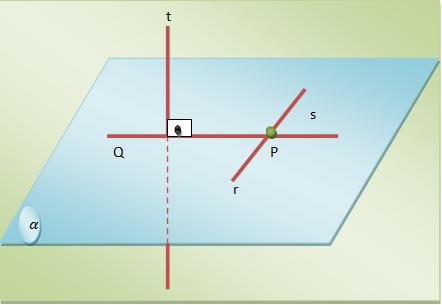
Consideramos uma reta perpendicular a um plano, se ela for perpendicular a todas as arestas do plano que passam pelo ponto onde ela o corta. Este ponto onde ela corta o plano denominamos de “pé da perpendicular”. Assim,
Teorema fundamental do perpendicularismo
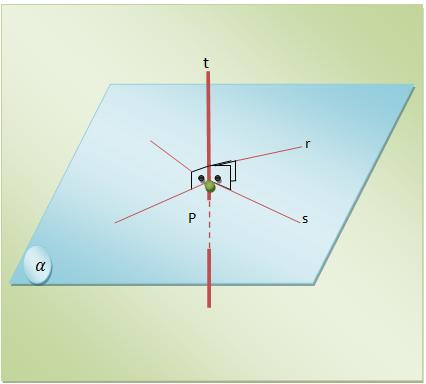
Para que uma reta seja perpendicular a um plano é preciso que crie um ângulo reto com duas concorrentes do plano.
Com as condições apresentadas neste teorema, temos os seguintes casos:
a) A reta t é considerada perpendicular às duas retas concorrentes do plano.
Assim,
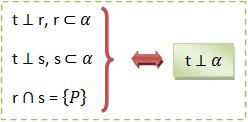
b) A reta t é considerada perpendicular a uma das retas concorrentes e ortogonal à outra.
Assim,
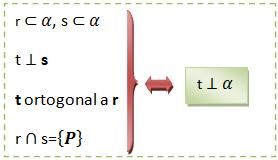
c) A reta t é considerada ortogonal às duas retas congruentes.
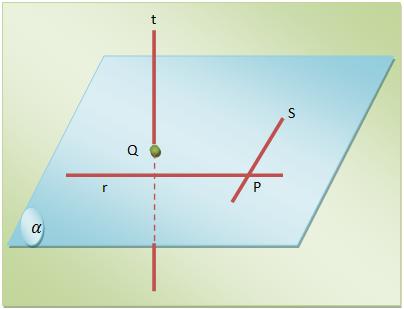
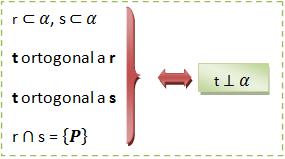
Lembrando que se uma reta é perpendicular a um plano de base, ela formará um ângulo reto com todas as retas do plano.
Teorema dos três perpendiculares
Considerando r perpendicular a α no ponto P, s contida em α deslizando por P, t contida em α não deslizando por P e perpendicular a s em Q.
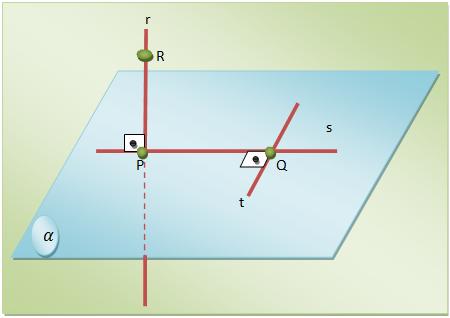
Ao afirmarmos que R é um ponto qualquer de r, poderemos dizer que a reta ![]() é perpendicular a t. Assim,
é perpendicular a t. Assim,
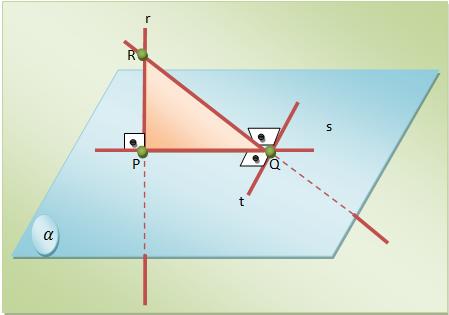

Propriedades do perpendicularismo de reta com plano
a) Chamamos de paralelas duas retas perpendiculares a um mesmo plano.
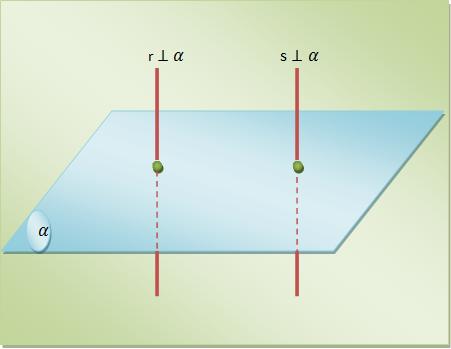
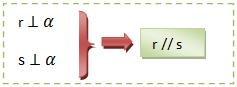
b) Chamamos de paralelos dois planos perpendiculares a uma mesma reta.
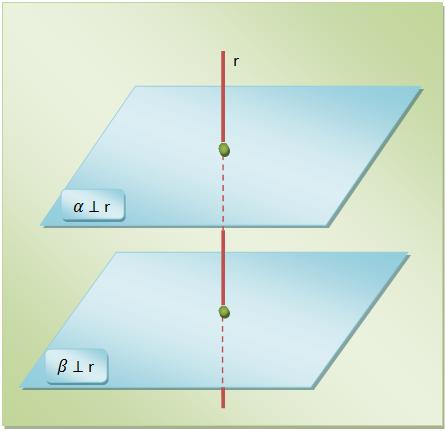
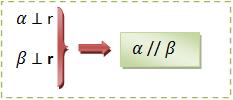
Plano perpendicular a plano
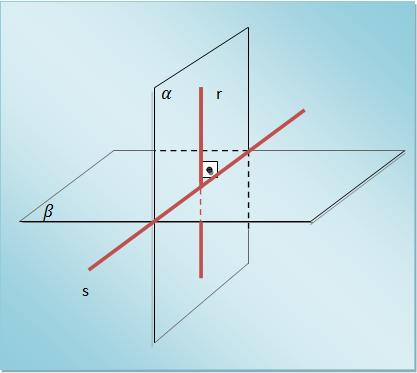
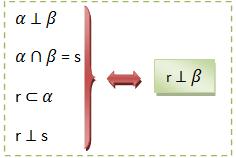
Podemos consideramos dois planos perpendiculares se, unicamente se, um deles possuir uma reta perpendicular ao outro.
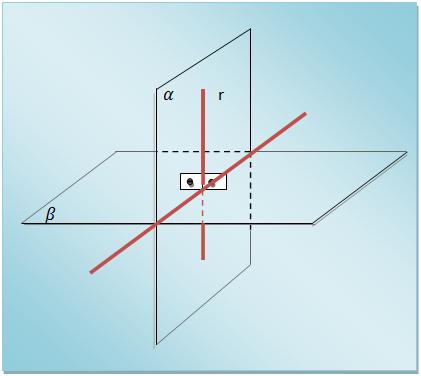
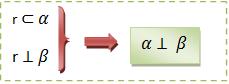
Propriedades do perpendicularismo do plano
a) Se considerarmos uma reta perpendicular a um plano, qualquer plano que a possua será perpendicular ao primeiro.
Assim,
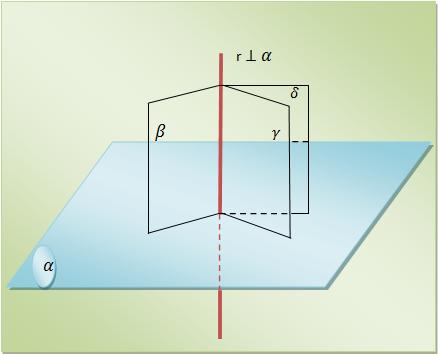
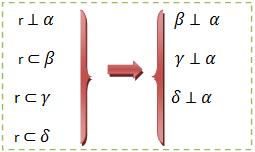
b) Se considerarmos que dois planos secantes são perpendiculares a um terceiro plano, o seu corte também será perpendicular a este terceiro plano.
Assim,
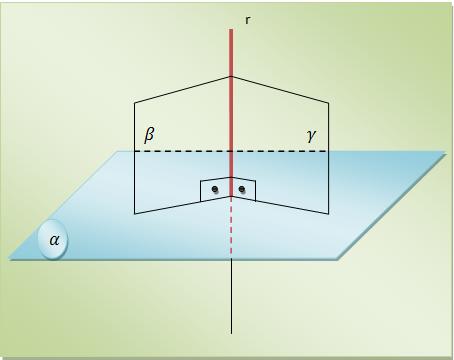
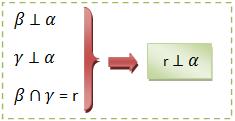
c) Se considerarmos que dois planos são perpendiculares, toda reta de um, perpendicular ao corte será perpendicular ao outro. Assim,