Progressão Geométrica (P.G)
Por Redação
Elas tratam de seqüências que podem representar crescimento de populações, cálculos de juros compostos, nascimento de novos galhos em uma árvore e tudo que aumente ou diminua segundo uma constante, a razão. Veremos que esta seqüência é “ mais rápida ” que a P.A tanto no crescimento como no decrescimento, pois sua razão é obtida pela divisão do termo pelo seu antecessor.
II – Formulário:
1o – Termo Geral:
an = a1 . qn-1
an = Termo geral
a1= 1º Termo
n = Número de termos
q = Razão
2 o – Propriedades:
1º) q = (a2 / a1 ) = (a3 / a2 ) = (a4 / a3) = constante
2º) a2 2 = a1 . a3
OBS: Se a1 = q temos ainda: a1 . a3 = a4
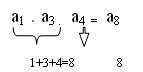
( A soma dos índices de cada lado devem ser iguais )
3o – Fórmula da Soma dos termos de uma P.G
a) P.G Finita: ( limitada)
Sn = [ a1 . (qn – 1)] / q – 1
b) Limite da soma de uma P.G infinita : (ilimitada)
Sn = a1 / 1 – q
O mais utilizado é o limite da soma da P.G infinita.
Os alunos confundem muito quando é necessário utilizar o termo geral ou a soma dos termos.
A dica é:
![]()
Numa seqüência, o termo geral fornece o valor naquela posição e a fórmula da soma fornece a soma de todos os termos, incluindo o daquela posição (limitada)
Ex.: no crescimento de uma comunidade que se comporta como P.G, o número de pessoas que nascem em determinado ano é obtido pelo an e o total de pessoas até aquele ano, incluindo aquele ano é o Sn.
4o – Produto dos termos de uma P.G. finita:
Pn = a1n . q n.(n-1)/2
OBS: A P.G pode ser aplicada para cálculos de matemática financeira quando se tratar de “juros sobre juros”, ou seja, juros compostos.
Ex. : Um valor V é aplicado a juros de 10% ao mês. Sendo juros compostos.
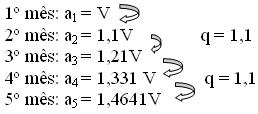
O termo geral fornece o valor acumulado (valor + juros) e q é ( 1 – a taxa ) se for desconto ou ( 1 + a taxa ) se for aumento.
