Ondas numa Corda
Por Redação
Aplicação
A função de uma onda é dada por: ![]() , onde x e y são medidos em cm e t em s. Determine a amplitude, o período, o comprimento e a velocidade de propagação da onda.
, onde x e y são medidos em cm e t em s. Determine a amplitude, o período, o comprimento e a velocidade de propagação da onda.
Solução:
Por comparação direta:
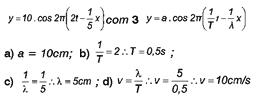
ONDAS NUMA CORDA
A velocidade v de propagação de um pulso (meia onda) que se propaga numa corda esticada depende da intensidade da força (T) que a traciona e da densidade linear (), conforme a fórmula de Taylor: ![]() . A densidade linear (m) é a relação entre a massa () e o comprimento (L) da corda: = m/L.
. A densidade linear (m) é a relação entre a massa () e o comprimento (L) da corda: = m/L.
Aplicação
Tem-se uma corda de massa 400g e de comprimento 5m, tracionada de 288N. Determine a velocidade de propagação de um pulso nessas condições.
Solução:
Dados: m = 400g = 0,4kg; L = 5m; T = 288N
A densidade linear da corda vale:

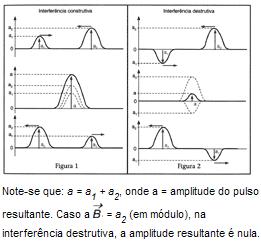
Interferência – Dois pulsos propagando-se numa mesma corda, em sentidos opostos, encontram-se em um determinado instante, produzindo a interferência. Segundo o Princípio da Superposição de Ondas, cada ponto da corda tem uma amplitude resultante igual à soma algébrica das amplitudes dos pulsos componentes. Após o encontro, de acordo com o Princípio da Independência das Ondas, cada pulso continua a se propagar como se nada tivesse ocorrido.
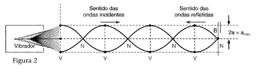
Ondas estacionárias – Originam-se da combinação dos fenômenos de reflexão e interferência e ocorrem devido à superposição de duas ondas idênticas (a incidente e a refletida) propagando-se em sentidos contrários.
No ventre (V), ocorre uma interferência construtiva de uma onda incidente com uma refletida (resultando na amplitude máxima da onda). No nó (N), ocorre uma interferência destrutiva (resultando em amplitude nula), ou seja, os nós não executam movimento oscilatório, impedindo a transmissão de energia, que fica confinada nos ventres.