O que são integral e derivada?
Por Victor Palandi
Para quem não é da área de exatas, determinados assuntos costumam parecer outro idioma, não é mesmo?
Entre esses conceitos estão o de integral e da derivada.
Você sabe o que ambos significam?
Acompanhe conosco, pois, neste texto, traremos informações que conceituem devidamente esses dois cálculos fundamentais da matemática
O que é integral?
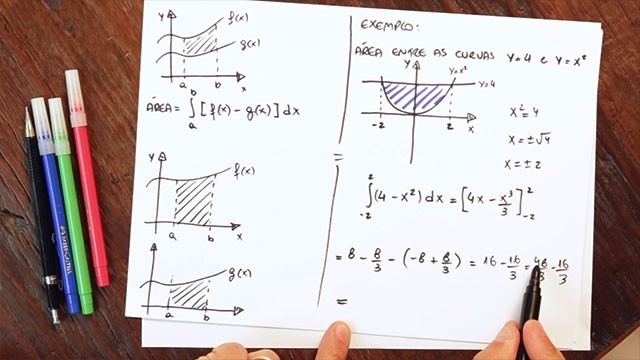
1# – Como a integral foi definida?
Dentro do conceito de cálculo, a integral foi criada de origem para delimitar a área localizada sob uma curva em um plano cartesiano.
O processo de cálculo da integrada é denominado integração. A integrada indefinida é chamada de antiderivada.
2# – Onde ela pode ser aplicada?
Além, é óbvio, da aplicação de tal conceito dentro dos problemas matemáticos, também é muito comum eles surgirem dentro de problemas de Física. Como, por exemplo, quando você precisa determinar a posição de um objeto em vários instantes, desde que sua velocidade instantânea seja conhecida em todos os instantes.
3# – Várias definições de integração
Existem inúmeras definições de integração.
De um modo geral, todas elas procuram resolver problemas conceituais diversos como aqueles que são relacionados à continuidade, limites e existência de determinados procedimentos que são usados na delimitação.
Tais delimitações são diferentes, porque há funções que podem ser integradas de acordo com uma definição, mas não podem com base em outra.
O que é derivada?

1# – Conceito de derivada
De forma bem conceitual, podemos chamar de derivada a taxa de variação de uma função.
Como o próprio nome dela já diz, a derivada representa de onde uma função veio, de onde ela deriva, o que deu origem a ela.
2# – Como ocorre sua aplicação?
Dessa maneira, a escolha certa do cálculo, sabendo fazer a interpretação correta, é a forma como a derivada é aplicada em um problema.
3# – Cálculos iniciais
Para que você entenda como funciona na prática, a derivada em um ponto de uma função y= f(x) está representada na variação instantânea de y com relação a x neste ponto em questão.
Um exemplo clássico também pode ser encontrado na física, onde uma função velocidade pode representar uma derivada (a taxa de variação) da função espaço.
É importante que, em todo cálculo matemático, você tenha a noção teórica do tema a ser trabalhado. Na matemática, é fundamental que você tenha todo o conhecimento teórico para saber implementar a aplicação no problema a ser resolvido. E um bom professor e/ou um bom método de estudo são essenciais para ajudar nisso.
