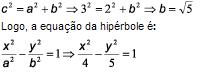Na figura, temos:

a) F1 e F2 são os focos da hipérbole, sendo = a distância focal.

b) A1 e A2 são os vértices da hipérbole, sendo A1A2 = A1F2 – A1F1 = 2a (constante da definição) →eixo real.

EQUAÇÃO DA HIPÉRBOLE COM CENTRO NA ORIGEM

Considere uma hipérbole na qual os focos pertencem ou ao eixo das abscissas ou ao eixo das ordenadas, e o centro é a origem O (0, 0). Considere também um ponto P (x, y) qualquer da curva. Com esses dados, obteremos, depois de alguns procedimentos matemáticos, a equação reduzida da hipérbole. 

Aplicações

01. Obter a equação da elipse de focos F1(-2,0) e F2(2,0), sabendo ainda que seu semi-eixo menor é b = 3.

Solução:

De início, note que os focos pertencem ao eixo Ox (isto é, o eixo maior é horizontal) e que a semidistância focal é igual a 2. Então:


02. Determinar a equação da hipérbole de focos F1(-3,0) e F2(3,0) cujo semi-eixo real é a = 2.

Solução

Das: coordenadas dos focos concluiu-se que a hipérbole tem seu eixo real situado no eixo Ox e que a semi distância focal é c = 3. Assim,